Z 変換 公式
フーリエ逆変換の公式は,時間関数 が角周波数 の成分 の.
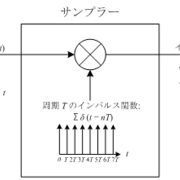
Z 変換 公式. 本章では,先ず9.1において,サンプリング定理を復習する.次に,9.2において,ディジタル信号処理におけるサンプラーの論理モデルとサンプル値の表現を,9.3 において Z 変換の導出を示す.そして 9.4 以降において Z 変換の定義,公式と定理,ラプラス変換の像関数からの Z 変換,差分方程式. 2.1 z変換の基礎 31 図2.3 z変換の収束領域 2.1.4 数列と収束領域 〔1〕 有限数列 数列x(n)は有限値であるとする。 X(z)= n2 n=n1 x(n)z−n (2.12) 収束領域としては,n1 < 0のとき,zp,p>0 の項を含むのでz = ∞ を除き, n2 > 0のときはzp,p<0の項を含むのでz =0を除く。 〔2〕 右側数列 ある時刻から,時間が進む. 86z 変換演習問題解答 部分分数展開法を用いて,逆z 変換x(n) を求める.X(z) を以下のように部分分数に分解する. X(z)= 1 1+1 16 z −4 (6.58) = 1 4 1 1− 1+j 2 √ 2 z−1 1 1− 1−j 2 √ 2 z−1 1 1− −1+j 2 √ 2 z−1 1 1− −1−j 2 √ 2 z−1 (6.59) よって x(n)= 1 4 1+j 2 √ 2 n + 1−j 2 √ 2 n + −1+j 2 √ 2 n + −1−j 2.
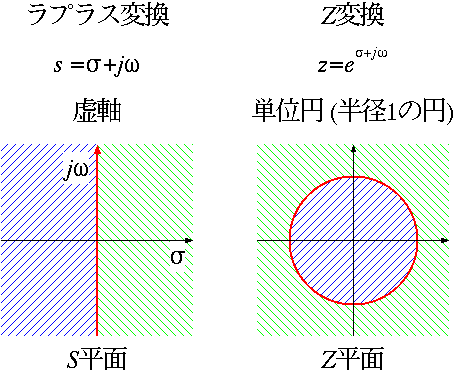
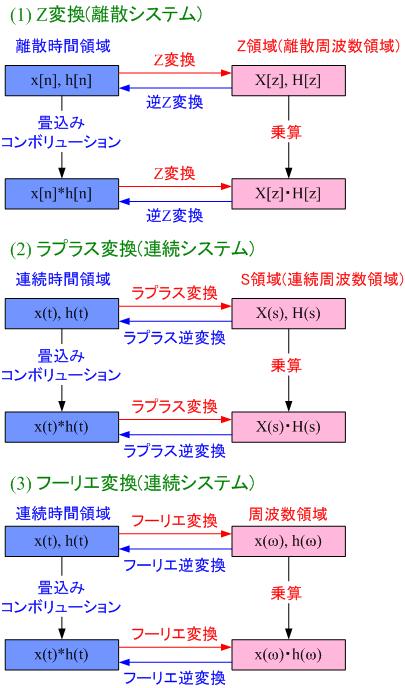
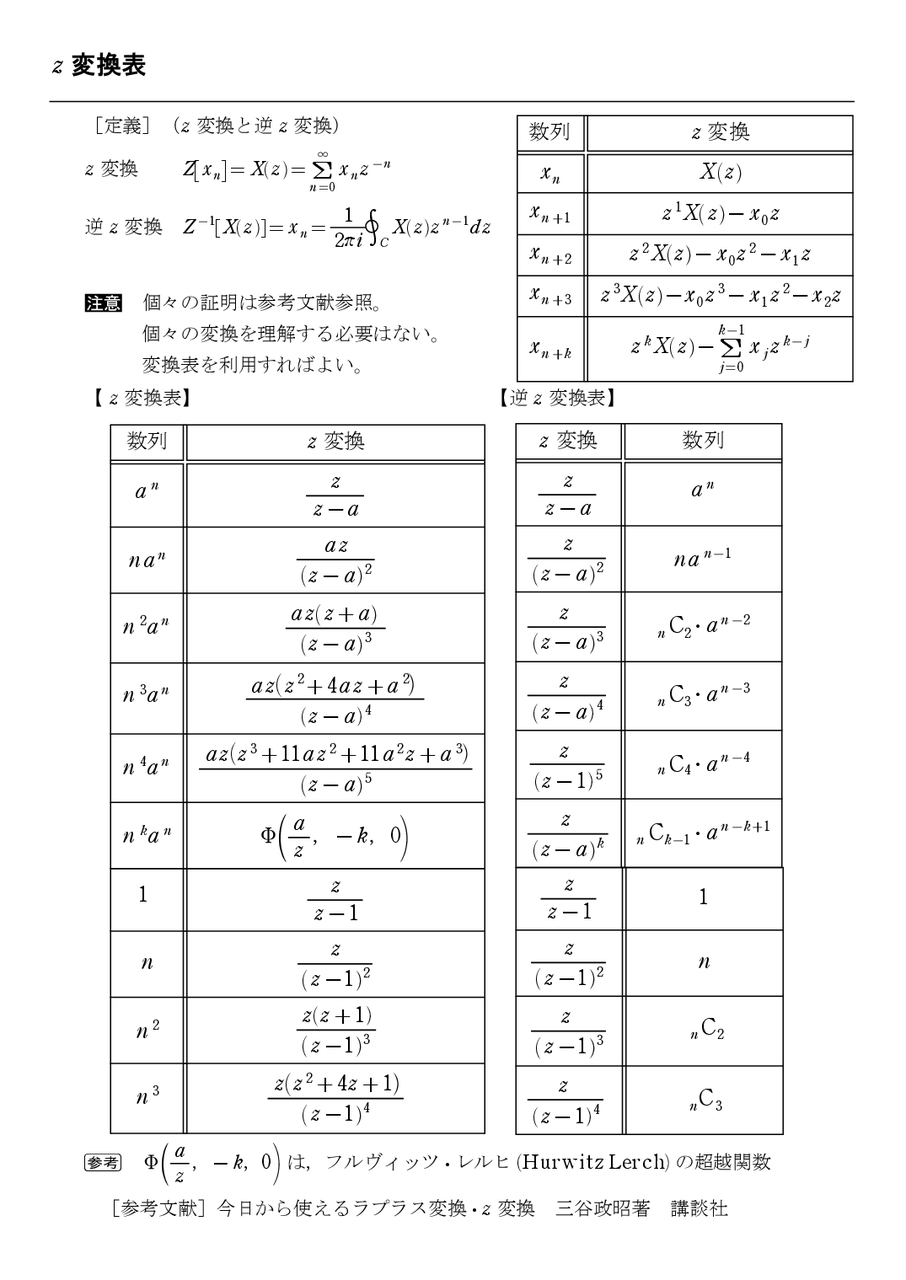
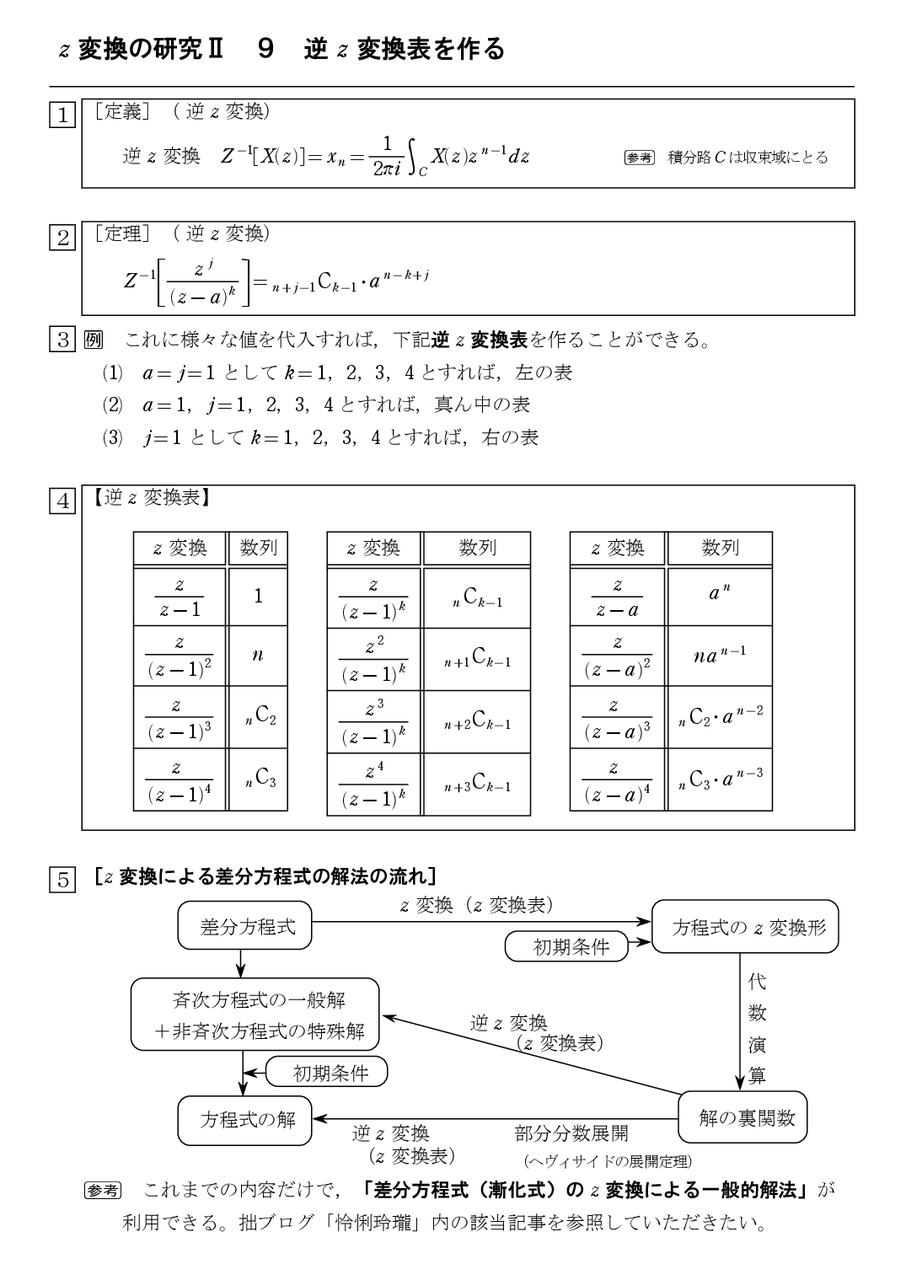
定義(z 変換と逆z 変換) z 変換 Z =X(z)=∑ z 逆z 変換 Z X(z)= = 1 2πi X(z)z dz 注意 個々の証明は参考文献参照。 個々の変換を理解する必要はない。 変換表を利用すればよい。 数列 z 変換 X(z) z X(z)− z z. 図2の場合、抵抗のパーセントインピーダンス(以下%z)は、下記の公式で求められます。 %z=zi/e×100% =pz/v 2 ×100% z:インピーダンスΩ i:電流a e:電圧v p:基準容量w 基準容量は自由に定義する場合と、自己容量基準で定義する場合があります。. ラプラス変換の\(f(t)\)をサンプリングした離散信号を\( x(n), z = e^{\sigma + i\omega T} \)とおくと、Z変換は次の式で表される。 $$ X(z) = \sum_{n=-\infty}^{\infty} x(n) z^{-n} $$ 逆Z変換は次の式で表される。 $$ x(k) = \frac{1}{2\pi i} \oint_{c} X(z) z^{k-1} dz $$.
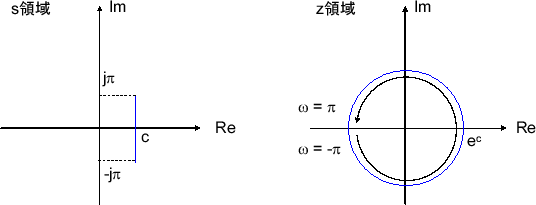
で表される変換をZ 変換(Z transform)といいます。 この式は、離散関数のフーリエ変換の式中の exp ( i T s ω ) ( T s は定数(サンプリング周期)、 ω は実数変数)の部分に z ( z は複素数)を代入したものになっています。. でも逆 z 変換の公式を使うのは面倒だお. やらない夫 なので,普通は何らかの式変形をした上で,z 変換表を見ながら置き換えていくのが常套手段だ.ラプラス変換のときと同じように,当面必要なものだけ抜粋しておこうか.. Z変換に関して 質問です。 u(n)=1(n >= 0) or 0(n < 0) (uは単位ステップ関数u(n)) をZ変換しなさいという問題なのですが、さっぱり解き方がわかりません(T_T) どのように考えたら良いのか導出方法を含めて回答をお願いしたいです。.
慶應義塾 理工学部 物理情報工学科 物理情報数学C 講師 足立修一 教科書 足立修一:信号・システム理論の基礎~フーリエ解析・ラプラス変換・z. 漸化式は、z変換の言葉ではシステムの信号伝達のダイナミクスであり、初項は初期状態である。 今から漸化式の両辺をz変換するのだが、両側z変換を使うと初期値すなわち初項の影響が消えてしまい、解が0になってしまうから、 右側 z変換を使う。. 電圧と電流は同相になる。 \(z_r=r\) Ω インダクタンス回路のインピーダンス.
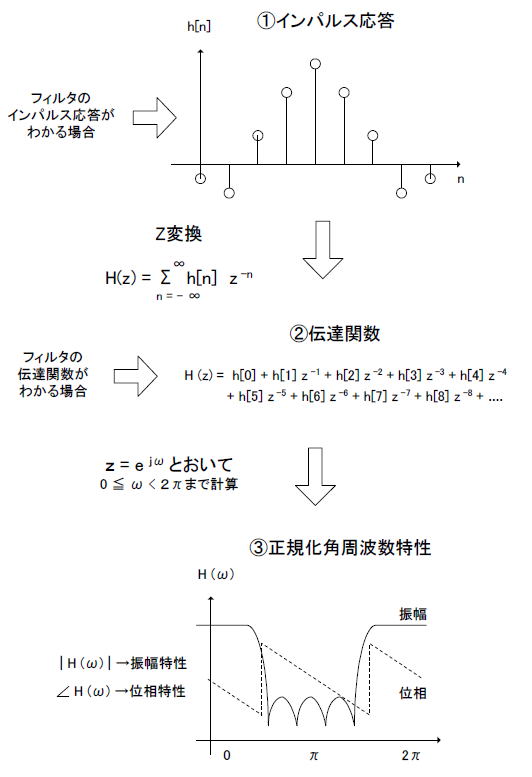
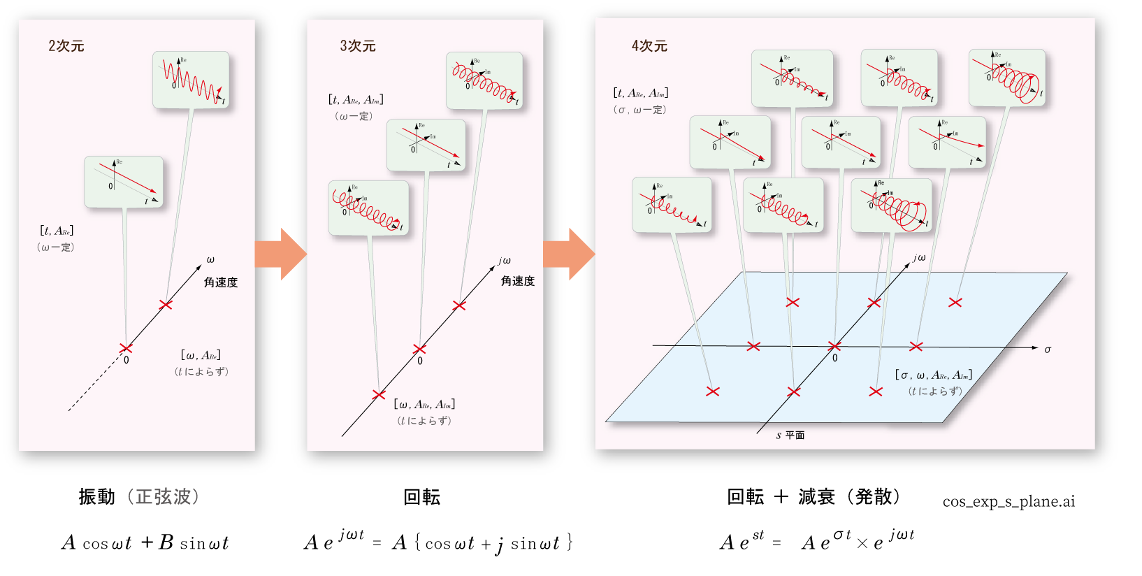
座標変換では sin と cos を使う。直交座標を極座標にするときは(2次元、3次元ともに)中心と座標の距離 r を最初に求める。 2次元. Z変換とは、()式に示すような変換式で、離散値パルス列を複素数z-n を含む関数に変換するものです。z-1 は、単位遅延演算子と言われ信号に単位遅延を与える演算子です。 z変換は、ディジタルフィルタの伝達関数や周波数特性を解析するのに用いることが出来ます。 ‹z変換に関する定理› z変換に関する定理を下記します。フーリェ変換と表記は異なりますが概念は. • 両側z 変換,片側z 変換ともにz 変換と呼ば れることがある.
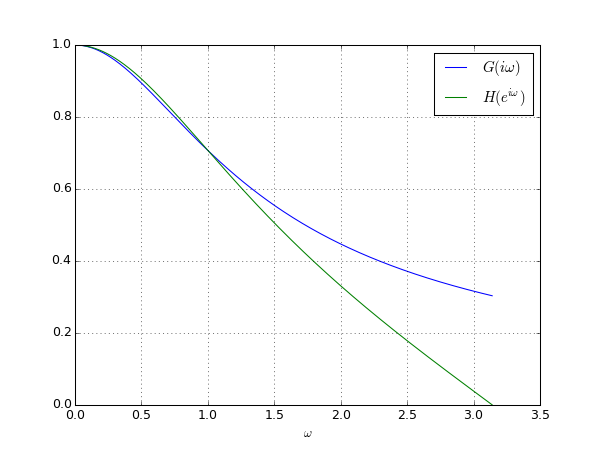
Z を e^{jωt} に書き換えれば、離散時間システムの周波数特性を. 高専4年の数学の教科書として使用した「新 応用数学」(大日本図書) のラプラス変換についての公式などを備忘録としてまとめたものです。 2.1 ラプラス変換の定義と性質 定義. %Zは,インピーダンスZ〔Ω〕に基準電流(定格電流)I B 〔A〕が流れて, 生じた電圧降下と基準電圧(定格電圧)E B 〔kV〕との百分率である。 次の式は、1項のΩ→%Z変換式である。 この式から%ZをΩに変換する式を算出すると、.
を {x n } の z変換 といいます。 z変換とラプラス変換は密接な関係があります。. Z 変換は,大雑把にいうと,微分方程式じゃなくて差分方程式用のラプラス変換だ.言い換えると,連続時間系で使われるラプラス変換に相当するものを離散時間系で考えたのが z 変換になる.. Z変換:離散系列でのラプラス変換のようなもの 形式的には次のとおり(zは複素数) X z =Zx n =∑ n=−∞ ∞ x n z−n (本によっては zn を掛ける定義もある) 無限級数なので収束しないかもしれない:収束性が問題 例1: x n =anu n X z =∑ n=−∞ ∞.
表1にz 変換の性質、表2にz 変換対を示す。 10.3 z逆変換の方法 z 逆変換の方法には留数の定理を用いる方法、べき級数展開法、部分分数展開法などがある。 a) べき級数展開法 ( ) ( ) ( ) A z B z X z = をz-1 のべき乗に展開 例10:. まず入力xnをZ変換する。 信号は2入力なので、 である。 次にhnをZ変換する。 次に畳み込みのZ変換は、 つまり、 これを逆Z変換すると. 極座標 (r, θ) から直交座標 (x, y) への変換.
ここでは、z変換について簡単に解説します。 z変換の定義を示します。 サンプル値列 {x n } ( n=0,1,2,‥) が与えられたとき、. チャープ z 変換 (czt) は、単位円以外の等高線に沿った z 変換の評価において有効です。チャープ z 変換は、また、素数長の変換の計算では dft アルゴリズムを使用するより効率的で、シーケンスの dft のサブセットを計算する際にも役立ちます。. • 以下しばらく,XZ =Zxのように,z変換前 の信号は英文字の小文字で書き, z 変換後の 信号は対応する大文字に右下付き添字 Z を 付けて表す.
ラプラス変換 公式一覧 Jan 4, 19 on Math. 差分方程式とz変換 差分方程式,漸 化式,z変 換,コ ンボリューション 浜田 望 1.は じめに 離散時間システムを記述する基本式である差分方程式 (漸化式)にz変 換を利用した解析や実現がどのように有 効に利用されているかについて述べる。特に代数的な手法. X n = Z − 1 X ( z ) = 1 2 π i ∮ C X ( z ) z n − 1 d z {\displaystyle x_{n}={\mathcal {Z}}^{-1}X(z)={\frac {1}{2\pi i}}\oint _{C}X(z)z^{n-1}\,dz}.
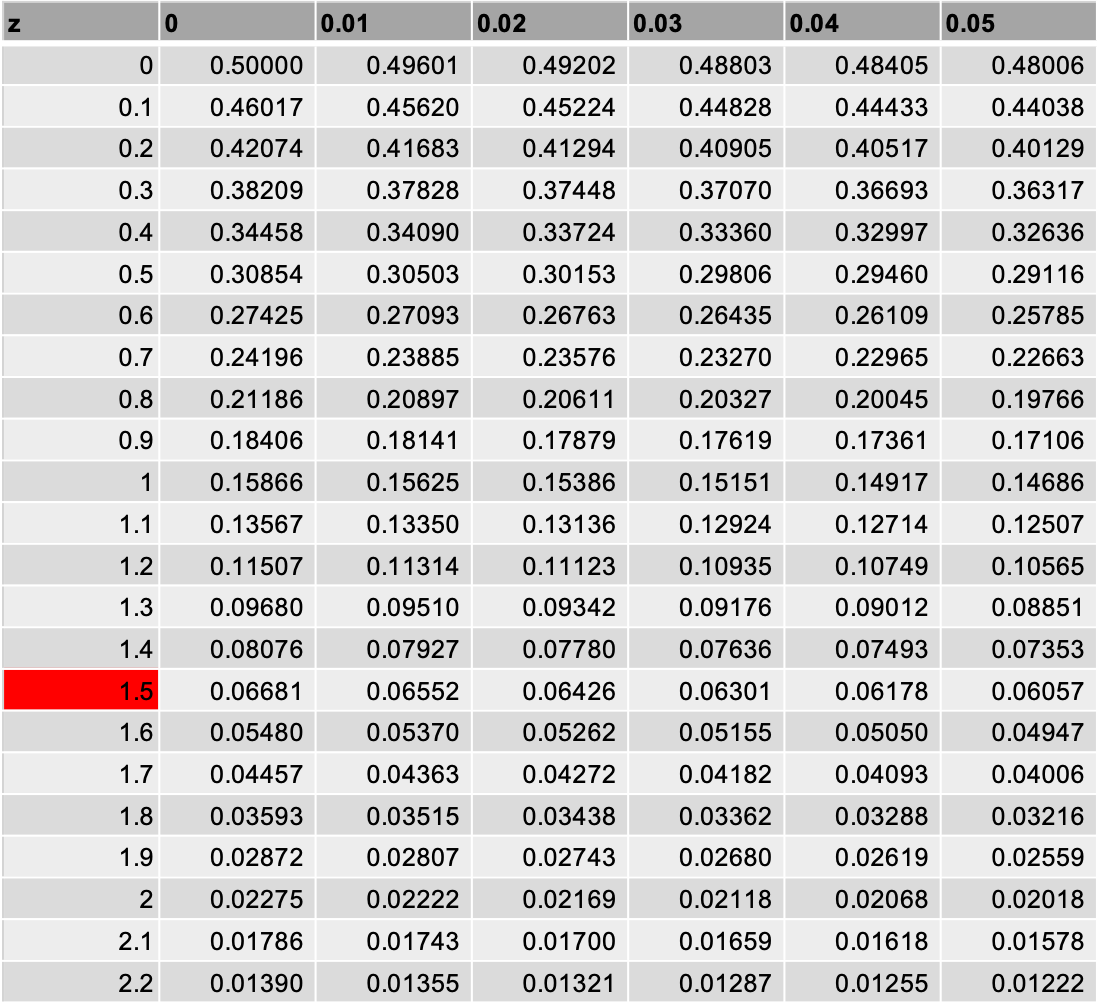
直交座標 (x, y) から極座標 (r, θ) への変換. と、分母がゼロになる地点z = z0 におけるf(z0)が結果として出てくる、という公式である。 (∵) 公式(91)の被積分関数をf(z) = f(z0) + (f(z) f(z0))のようにz0 における値f(z0)とその 値からのずれf(z) f(z0)に分離して書くと I C f(z) z z 0 dz = I C f(z0) z z dz + I C f(z) f(z0) z z0 dz (92) 被積分関数は、経路C 内でz = z0 を. 標準化と”Z” こちらも「データの変量変換」で扱った、『標準化』の確率変数バージョンです。(正規分布の記事で利用します。) $$\mathrm{EZ=\frac{X-μ}{σ^{2}}}$$ 性質も、変換後の期待値=0、分散=1と同じで証明方法もほとんど共通しています。 E (X)やV(X)の公式.
A_{n-1} は z^{-1} A(z) (このため、z^{-1} は遅延演算子と呼ばれる) a_{n+1} は z A(z) a * b (たたみこみ) は A(z) B(z) のように変換する。z 空間での代数的な演算を経たのちに. 〔〔〔〔5555〕〕〕〕有限長の信号の有限長の信号の有限長の信号のz zzz変換は簡単変換は簡単変換は簡単 −= − =⋯+ − + − + + + +⋯+ +⋯ ∞ =−∞ ∑ n k n X z( ) ( ) x n z x ( 2) z x ( 1) z x (0) z0 x (1) z1 x (2) z2 ( ) x k z 例: = = = = ⋯それ以外 ⋯ ⋯ ⋯ 0 1 2 2 1 3 0 ( ) n n n x n → X z z z( ) 3 2= + +− −1 2. Z変換と呼ばれる変数変換を行う。 統計の分野でのz変換は、離散系の電子分野で使うz変換とは全く異なる。実にまぎらわしい。 統計ではこのz変換により、基準になるたった一つの正規分布として平均値がゼロ、 分散が1の標準化正規分布が得られる。.
X z( ) がzの有理関数(分母と分子が多項式であるような関数)になることが多い。 有理関数の逆 z 変換 〔1〕べき級数展開 z 変換の定義式: = =⋯+ − +⋯+ + −+ − +⋯ ∞ =−∞ X z( ) ∑( ) x n z − x( )k z k x (0) x (1) z 1 x (2) z 2 n n なので, X z( ) が, = =⋯+ +⋯+ + −+ − +⋯ − ∞ =−∞ ∑− 2 2. YーΔ変換およびΔーy変換公式の導出の考え方は、下図の合成抵抗公式の導出と同じである。 上図の抵抗r 1 とr 2 を一つの合成抵抗r 12 に等価変換できる条件は、等価変換前後で電流が変わらないことである。. 2 4 1 X( ) 3 2 + + − = z z z z (10.15).
シンボリック関数の z 変換を計算します。 1 番目の引数がシンボリック関数を含む場合、2 番目の引数はスカラーでなければなりません。 syms f1(x) f2(x) a b f1(x) = exp(x);.

第10回 Z変換

Z 変換 離散的ラプラス変換 の研究 1 概要と予告 怜悧玲瓏 高校数学を天空から俯瞰する

ラプラス変換とフーリエ変換 半導体事業 マクニカ
Z 変換 公式 のギャラリー
2
スマホで学ぶ 実践ディジタル信号処理入門

第10回 Z変換

ディジタル信号処理 Digital Signal Processing Ppt Download

ラプラス変換とその使い方1 基礎編 ラプラス変換とは何か 変換の基礎事項は 音声付き電気技術解説講座 公益社団法人 日本電気技術者協会
標準正規分布表の見方や使い方 標準化やz値の計算式はどうすればいい いちばんやさしい 医療統計

Z 変換 怜悧玲瓏 高校数学を天空から俯瞰する

ヤコビの虚数変換式 Wikipedia

Z変換 s領域から離散領域に変換 によるプログラム 技術メモ
Http Www Challenge Jtex Com Index Php Dispatch Attachments Getfile Attachment Id 299

Z変換 s領域から離散領域に変換 によるプログラム 技術メモ

Z変換
Z Transform

第10回 Z変換
スマホで学ぶ 実践ディジタル信号処理入門
重積分の変数変換とヤコビアン リーマン空間における多重積分

Z変換 s領域から離散領域に変換 によるプログラム 技術メモ
ラプラス変換とz変換
Http Granite Phys S U Tokyo Ac Jp Tsubono Hiramatsu Seminar 93d 8eq F1 98h 81i10 8f Cd 8eb 81j Pdf
ローラン展開 複素積分の例題 Sinz Z Cosz Z Tanz Z 2 など三角関数型 ばたぱら
重積分の変数変換とヤコビアン リーマン空間における多重積分

3次元cgと座標系

ラプラス変換 Wikipedia

双一次変換 Wikipedia
Http Www Ssc Pe Titech Ac Jp Lectures Signalandanalysis Signalsandsystemsanalysis10 Pdf

信号 システム理論の基礎 フーリエ解析 ラプラス変換 Z変換を系統的に学ぶ コロナ社
Annex Jsap Or Jp Photonics Kogaku Public 13 04 Kenkyu1 Pdf
14 Z 変換 やる夫で学ぶディジタル信号処理

Z変換をやさしく教えて下さい 音響学入門ペディア
Http Www Ssc Pe Titech Ac Jp Lectures Signalandanalysis Signalsandsystemsanalysis10 Pdf
Http Www Ssc Pe Titech Ac Jp Lectures Signalandanalysis Signalsandsystemsanalysis10 Pdf

一次 Iir Lpf の簡易設計 An Engineer19のブログ

5分でわかる ローレンツ変換 特殊相対性理論の要を理系ライターがわかりやすく解説 ページ 2 3 Study Z ドラゴン桜と学ぶwebマガジン

2 の途中でなぜ底の変換公式でlog2にすることを決定したのかがわかりません 教え Clear
Http Www Cqpub Co Jp Interface Sample 0609 I Pdf
14 Z 変換 やる夫で学ぶディジタル信号処理
2

Z変換 s領域から離散領域に変換 によるプログラム 技術メモ
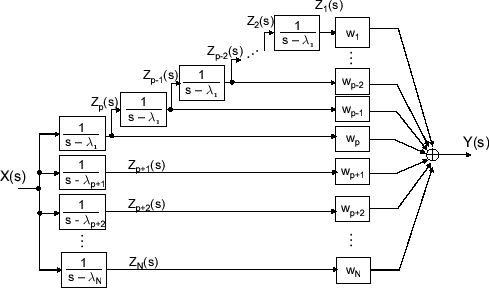
A 伝達関数の部分分数展開 やる夫で学ぶディジタル信号処理
14 Z 変換 やる夫で学ぶディジタル信号処理
漸化式を Z 変換で解く方法 2 定義と表 怜悧玲瓏 高校数学を天空から俯瞰する
Http Www Ssc Pe Titech Ac Jp Lectures Signalandanalysis Signalsandsystemsanalysis10 Pdf

Z 変換 怜悧玲瓏 高校数学を天空から俯瞰する

スマホで学ぶ 実践ディジタル信号処理入門
Q Tbn 3aand9gctspqsb0gfmq61pydrj Qnshlpcjfjvzus4h8c4spvb30mu2 Fx Usqp Cau
14 Z 変換 やる夫で学ぶディジタル信号処理
座標回転公式と球面三角法
Q Tbn 3aand9gcrx3vpexakw3jrzutzlajva0g Vb2efthacskef0 Gq65h3jshu Usqp Cau
宮崎技術研究所 自動制御講座 4 1 3 Z変換とパルス伝達関数 1 2
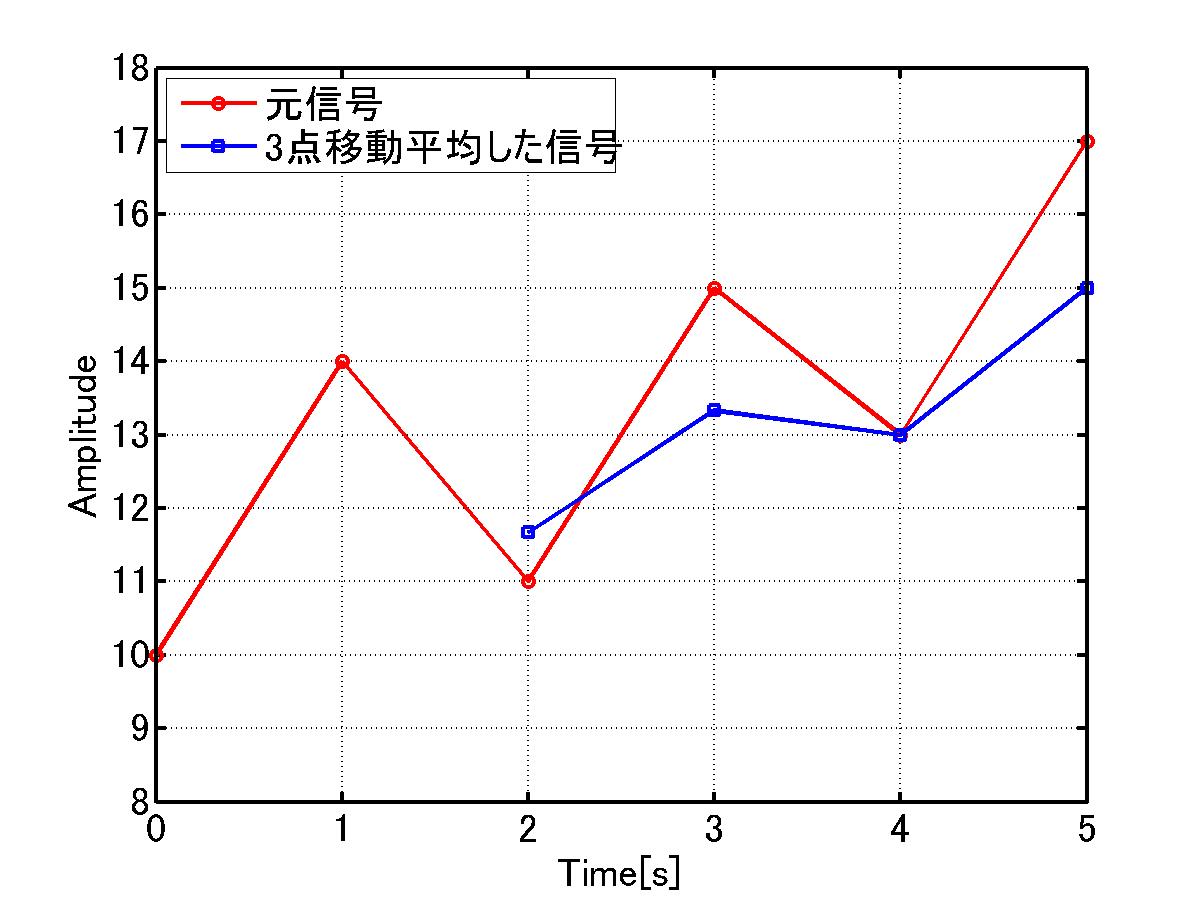
移動平均

Z変換をやさしく教えて下さい 音響学入門ペディア

双一次変換とは 制御工学の基礎あれこれ

Ppt デジタル信号処理 Powerpoint Presentation Free Download Id
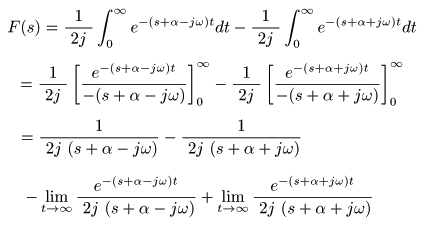
ラプラス変換
Http Www Ssc Pe Titech Ac Jp Lectures Signalandanalysis Signalsandsystemsanalysis10 Pdf
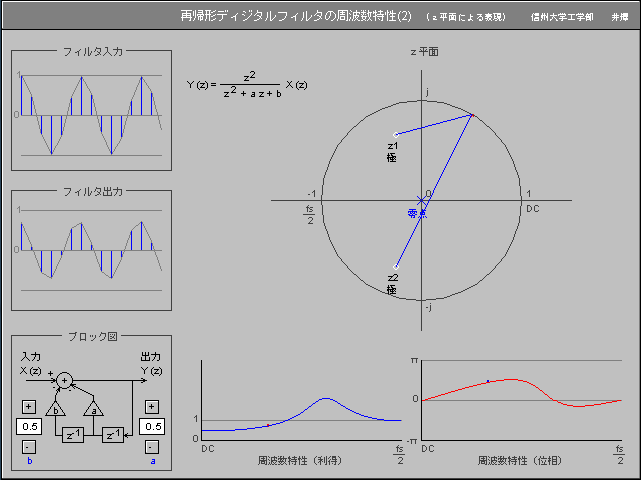
ディジタルフィルタとz変換
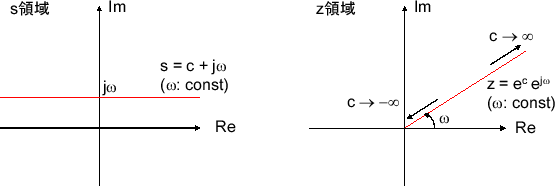
14 Z 変換 やる夫で学ぶディジタル信号処理
Onsen Mula Org Wp Content Uploads 17 04 Digital Control 10 Pdf
ディジタルフィルタの作り方 Qiita

双一次変換のクセ S Z伝達関数変換 パワエレ学生の備忘録

オンラインマセマティカを気軽に使う 15 逆z変換 怜悧玲瓏 高校数学を天空から俯瞰する

ラプラス変換とフーリエ変換 半導体事業 マクニカ

双一次変換とは 制御工学の基礎あれこれ

高校数学 複素数平面上の反転変換w 1 Zによる像 受験の月

Z 変換の研究 5 Z 変換表を作る 怜悧玲瓏 高校数学を天空から俯瞰する

驚異のラプラス変換 微分方程式やフーリエ変換との関係は Gis 空間情報クラブ 株式会社インフォマティクス

第10回 Z変換
App Mathsoc Jp Download Abstract Tsukuba16mar Tsukuba16mar 11 03 Pdf
9 ディジタル信号処理と Z 変換 趣味人のブログ
Http Leo Ec T Kanazawa U Ac Jp Staffs Nakayama Edu File Signal Proc Ch2 Pdf

26 3 相関係数 統計学の時間 統計web

高校数学 変数変換と標準化 偏差値 受験の月

6 ラプラス変換 Ppt Download
Q Tbn 3aand9gctt73u7mruab9oofmdrskbvy74zyibs6l5hjnmfebp6x 54qyhl Usqp Cau
ラプラス変換

デジタル信号処理 Ppt Download
Z 変換 怜悧玲瓏 高校数学を天空から俯瞰する
Q Tbn 3aand9gcqmff Xgo5ufz5l 3thaos0cebyivwccjygvwtr4 Xrpccwiqfj Usqp Cau

第10回 Z変換

Z 変換の研究 5 Z 変換表を作る 怜悧玲瓏 高校数学を天空から俯瞰する

9 ディジタル信号処理と Z 変換 趣味人のブログ
Http Www Ssc Pe Titech Ac Jp Lectures Signalandanalysis Signalsandsystemsanalysis10 Pdf

宮崎技術研究所 自動制御講座 4 1 3 Z変換とパルス伝達関数 1 2

ディジタル信号処理 Digital Signal Processing Ppt Download
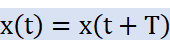
フーリエ変換とdftの関係

Z変換をやさしく教えて下さい 音響学入門ペディア
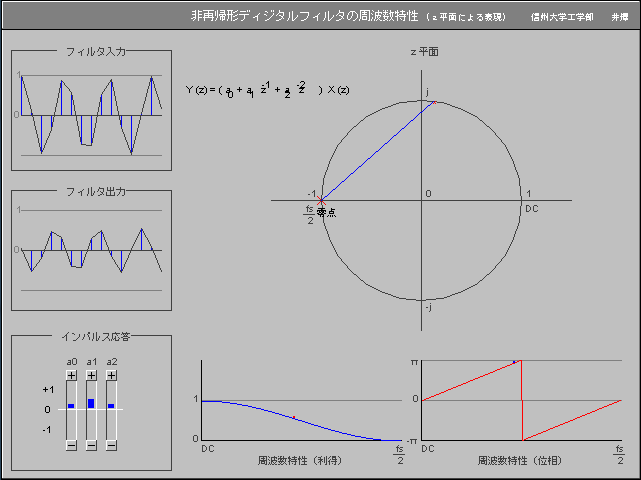
ディジタルフィルタとz変換

Z 変換の研究 20 自然数の R 乗和の公式 怜悧玲瓏 高校数学を天空から俯瞰する

26 3 相関係数 統計学の時間 統計web
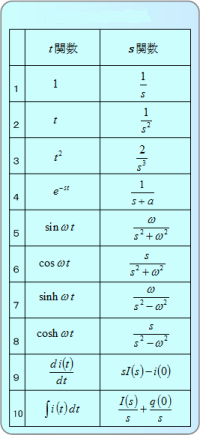
ラプラス変換とその使い方2 過渡現象編1 直流rl回路の過渡現象 音声付き電気技術解説講座 公益社団法人 日本電気技術者協会

Z変換 s領域から離散領域に変換 によるプログラム 技術メモ
ディジタル制御の基礎
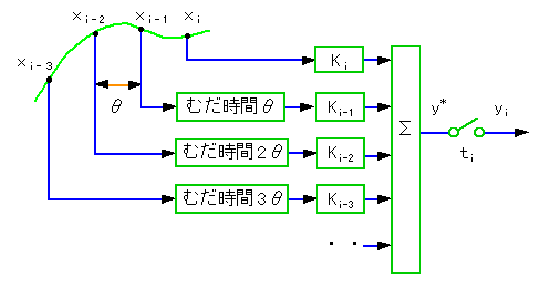
宮崎技術研究所 自動制御講座 4 1 3 Z変換とパルス伝達関数 1 2

ラプラス変換とフーリエ変換 半導体事業 マクニカ

Z 変換の研究 3 ラプラス変換と Z 変換 怜悧玲瓏 高校数学を天空から俯瞰する
Onsen Mula Org Wp Content Uploads 17 04 Digital Control 10 Pdf

2 の途中でなぜ底の変換公式でlog2にすることを決定したのかがわかりません 教え Clear

9 ディジタル信号処理と Z 変換 趣味人のブログ
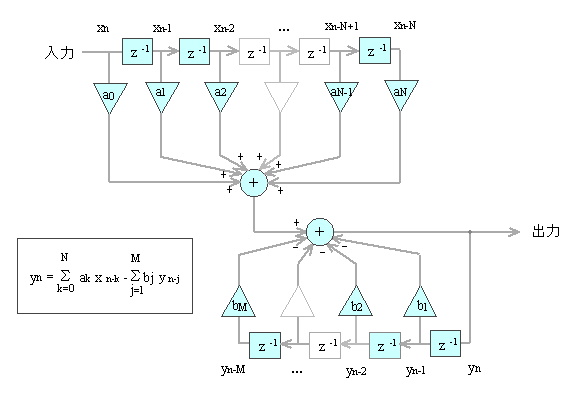
ディジタルフィルタとz変換

3次元cgと座標系

Z 変換 怜悧玲瓏 高校数学を天空から俯瞰する



